Détecter de l’adaptation dans les populations structurés : fastoche, non?

Je suis bien content de vous annoncer qu’un nouvel article issu de la thèse de Priscila Salloum est maintenant publié (en avant-première !) dans Journal of Animal Ecology ! L’idée de la thèse de Priscila (à l’Université d’Auckland, co-dirigée par Shane Lavery et Anna Santure et, bah, moi-même) était d’utiliser des données génomiques et morphométriques pour caractériser et mieux comprendre la diversité chez un mollusque marin de Nouvelle-Zélande, qu’elle a choisi comme étant le magnifique Onithochiton neglectus.

Priscila avait déjà analysé des données génétiques montrant que cette espèce possède une étrange structure de populations : les populations de l’île du Nord de la Nouvelle-Zélande, qui sont géographiquement plus proches, sont très éloignées génétiquement parlant, et les populations de l’île du Sud, des îles Chatham et des îles sub-antarctiques sont beaucoup plus proches, génétiquement.

En général, on observe plutôt que la différenciation génétique suit les distances géographiques, tout simplement parce que les populations les plus éloignées ont tendance à échanger moins de migrants. Donc, que se passe-t-il ici ?

En fait, ça s’explique très bien par le fait que cette espèce de chiton est capable de voyager à dos de varech (sur l’espèce d’algue Durvillea antarctica). Et comme ça, les espèces des îles subantarctiques sont, en fait, mieux « connectées » par les grands courants océaniques que les populations nordiques, qui sont certes plus proches géographiquement, mais aussi plus isolées, notamment en raison de boucles dans les courants locaux.

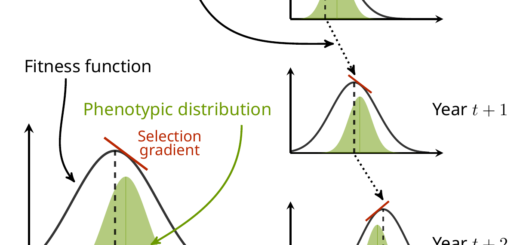
OK, bon, passons maintenant à la question qui nous occupe, et à pourquoi je vous parle de tout ça. Je parle de détecter de l’adaptation locale, mais c’est quoi ce machin ? L’adaptation locale se produit lorsque différentes populations d’une espèce sont soumises à des différences dans leur environnement local, ce qui génère une sélection différente selon les populations. Si les bonnes conditions sont réunies, alors les populations vont changer dans leur composition génétique pour répondre à cette sélection locale, et donc (par définition en fait…) elles vont s’adapter ! C’est ça qu’on appelle « adaptation locale ». Et en théorie, il devrait être possible de détecter les localisations dans le génome (ou locus) qui sont impliquées dans cette adaptation locale. Pour ce faire, il y a deux options principales : détecter les locus qui sont particulièrement différenciés entre les populations (enfin, plus que le reste du génome quoi) parce qu’ils ont répondu à la sélection, ou essayer de corréler les fréquences des variants à chaque locus avec une variable environnementale.

Très bien, OK, mais alors « structure de la population », c’est quoi et ça vient faire quoi là-dedans ? Imaginez que vous vouliez trouver des gènes qui sont liés à la couleur des yeux. Vous pourriez étudier un groupe de gens aux yeux bleus et un autre groupe aux yeux bruns, et toute variation génétique fortement liée à l’appartenance au groupe des yeux bleus ou bruns doit être liée à la couleur des yeux, n’est-ce pas ? Peut-être en effet, mais que se passe-t-il si votre « groupe aux yeux bleus » est composé de Suédois et que votre « groupe aux yeux bruns » est composé de Japonais ? Ça paraît évident (et bien que les groupes ethniques partagent une grande partie de leur génome !), il existe tout de même un certain nombre de locus dans le génome qui diffèrent entre les groupes de Suédois et de Japonais sans avoir le moindre lien avec la couleur des yeux ! Conclure que tous ces locus influencent la couleur des yeux serait commettre un grand nombre de faux positifs.Et donc lorsqu’on cherche une association génétique avec des caractéristiques phénotypiques comme celle-là, ou lorsque l’on cherche des signaux de sélection dans le génome, on essaie de bien tenir compte de la « structure de la population », c’est-à-dire du fait que les individus n’appartiennent pas à un même groupe homogène, mais à des groupes plus ou moins différenciés (que ce soit au sein des populations ou entre elles).

Le problème, c’est que j’ai montré il y a quelque temps que les méthodes de criblage génomique pour détecter la sélection souffrent d’un très fort problème de faux positifs lorsqu’elles sont exposées à une forte structure de population, et ce même lorsqu’elles sont censées corriger ladite structure de population (pour le résumer rapidement : c’est vraiment plus facile à dire qu’à faire !). Et donc, lorsque nous avons été confrontés à ce problème dans le vrai monde avec cette espèce de chiton, dont les populations sont fortement distinctes, nous avons utilisé trois approches pour diminuer la proportion de faux positifs parmi nos résultats positifs. La première approche était très simple : nous avons distingué les populations extrêmement différenciées du Nord de celles du Sud, moins différenciées. La seconde consistait à simuler une variable environnementale complètement aléatoire. Si les locus sont souvent associés de manière significative à une variable parfaitement arbitraire qui n’existe en ce monde que parce qu’elle provient d’un programme informatique, c’est à peu près certain que le fait que toute « association » doit être regardée avec un air circonspect. Bien sûr, ça ne veut pas dire que le locus n’est pas soumis à la sélection (il pourrait tout à fait l’être !), mais plus simplement qu’il s’avère que notre test statistique n’était vraiment, mais vraiment, pas informatif !

La troisième approche consistait à utiliser plusieurs méthodes et à combiner leurs résultats. J’ai montré dans l’étude ci-dessus que combiner ces méthodes permet d’enrichir nos résultats en vrais (plutôt que faux) positifs. Mais utiliser l’intersection des méthodes (toutes les méthodes doivent être d’accord sur le fait qu’un positif est positif) comme je l’ai fait à l’époque, c’est un critère très (trop) strict et ça ne m’a jamais vraiment satisfait. Une solution serait de faire une sorte de moyenne… Mais l’utilisation de la moyenne arithmétique est super insatisfaisante, parce qu’elle donne beaucoup de poids aux tests non positifs (tout comme l’utilisation de la moyenne harmonique favoriserait les tests positifs). La moyenne géométrique (la plus équilibrée des trois) serait donc la plus appropriée ? Un argument plus technique (désolé…) en faveur de la moyenne géométrique est qu’elle peut être considérée comme une moyenne (classique, donc arithmétique) sur l’échelle log (ce que ça veut dire, c’est qu’on prend le logarithme de notre variable et qu’on travaille avec ces nouvelles valeurs). Il se trouve que c’est une super échelle pour interpréter la significativité des tests (les trucs comme la p-valeur ou la q-valeur). Bien que j’aie vérifié le comportement de cette méthode sur de vieilles simulations, il faudrait un jour que je m’attaque à cette idée avec une étude de simulation dédiée !

On a donc mis en œuvre toutes ces raffinements dans le but de réduire nos problèmes de faux positifs. Et on a réussi à passer de centaines, voire de milliers de locus qui auraient pu être considérés comme positifs, à seulement 86. Bon, bien sûr, en chemin, on a très certainement éliminé certains locus « vraiment positifs » qui auraient pu être intéressants. Mais comme la vie c’est pas facile, il n’y a (par définition…) aucun moyen de distinguer un faux d’un vrai positif (sauf à tout tester expérimentalement !), et la seule chose que nous pouvons faire est d’enrichir notre ensemble de locus finaux en vrais positifs par rapport aux faux positifs. C’est ce que nos petites approches filtrantes ont visé à faire, mais il paraît clair que nous avons encore besoin de méthodes encore plus performantes pour résoudre ce soucis très répandu !