Il y a plus d’évolution en populations naturelles qu’on ne pensait

Publié · Mis à jour

Voilà qui n’est pas vraiment connu du grand public, mais la théorie de l’évolution est en fait très fortement mathématisée. Par exemple, il existe un théorème nommé « L’équation de Price » qui décrit de manière générale comment les propriétés biologiques évoluent en réponse à la sélection.

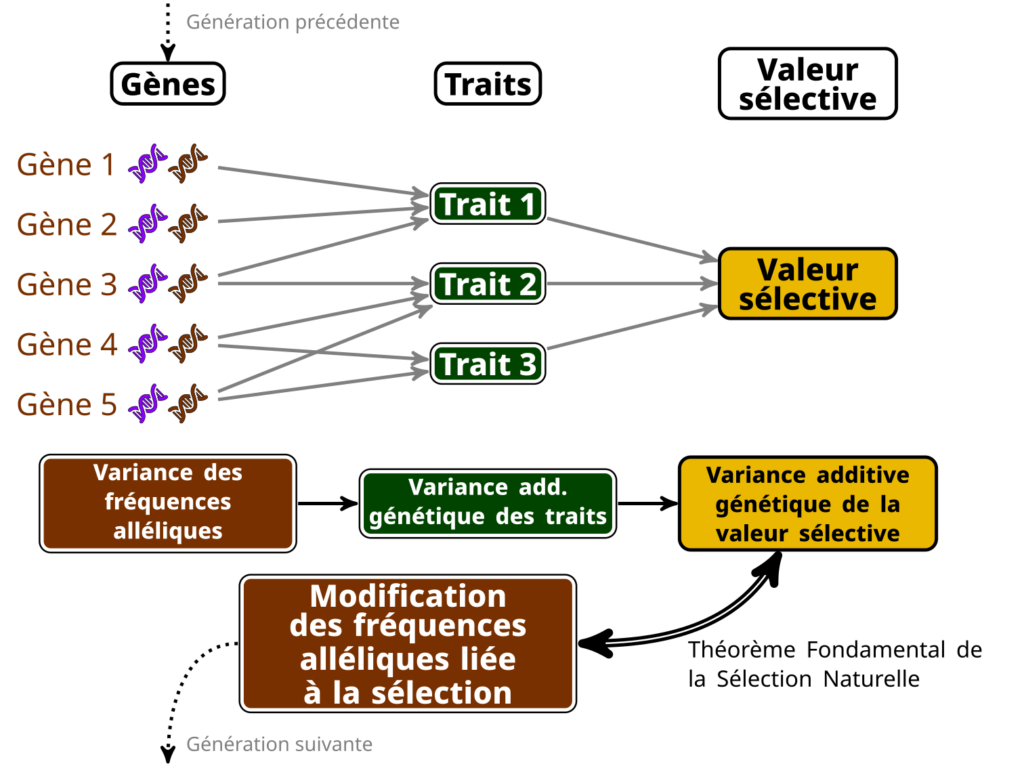
Ronald Fisher (un gars pas très souriant…)

Ronald Fisher a été l’un des premiers promoteurs d’une théorie de l’évolution mathématisée (au milieu d’autres choses plus embarrassantes dont il faisait la publicité…), et il a même nommé (un peu pompeusement) une équation le « Théorème Fondamental de la Sélection Naturelle ». Ce théorème a fait l’objet de beaucoup de polémiques et d’interprétation diverses. Mon interprétation favorite (un peu simpliste, mais pas trop fausse), c’est qu’il est possible de connaître la quantité de changement au niveau génétique attendu à cause de la sélection en calculant la quantité de variance de la valeur sélective (relative) qui est transmissible à la génération suivante, que l’on nomme « variance génétique additive de la valeur sélective ».

Dit autrement, si on peut calculer cette fameuse variance additive génétique de la valeur sélective, on a accès à une estimation directe de l’ampleur de l’adaptation (dans le sens : ampleur des modifications des fréquences alléliques d’une génération sur l’autre, liées à la sélection). Ça vient du fait que cette variance est (plus ou moins) liée à la variance des fréquences alléliques des gènes sous sélection (c’est-à-dire les gènes dont les variations impactent des traits sous sélection). J’ai essayé de résumer ça dans la petite infographie ci-dessous…

Les gènes influençant les différents traits phénotypiques (les caractéristiques des êtres vivants quoi) importants pour la sélection ont des allèles différents, ce qui signifie qu’il existe une certaine « variance des fréquences alléliques » dans la population. Pour rester trèèèèèèès simple, on peut dire que ce que nous appelons la « variance génétique additive » des traits est liée à cette variance des fréquences alléliques (ainsi qu’à l’impact de chaque gène sur les traits). À leur tour, ces traits influencent la capacité et la manière dont les individus se reproduisent, et donc leur valeur sélective. En fin de compte, la « variance génétique additive de la valeur sélective » est liée à la fois à la variance des fréquences alléliques de ces gènes et à la façon dont les individus se reproduisent. Avec un peu de mathématiques (que je vais vous épargner ici, de rien, ça me fait plaisir), on peut montrer que cette « variance génétique additive » de la valeur sélective est liée au changement attendu des fréquences alléliques d’une génération à l’autre dû à la sélection, et donc au total de l’adaptation « en cours » dans la population.

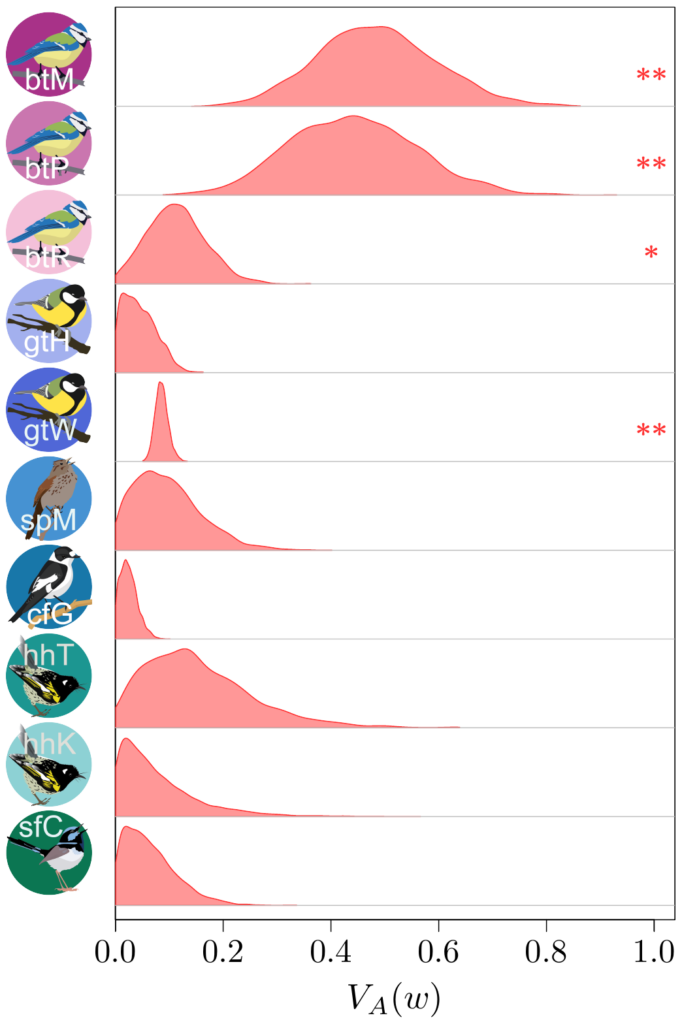
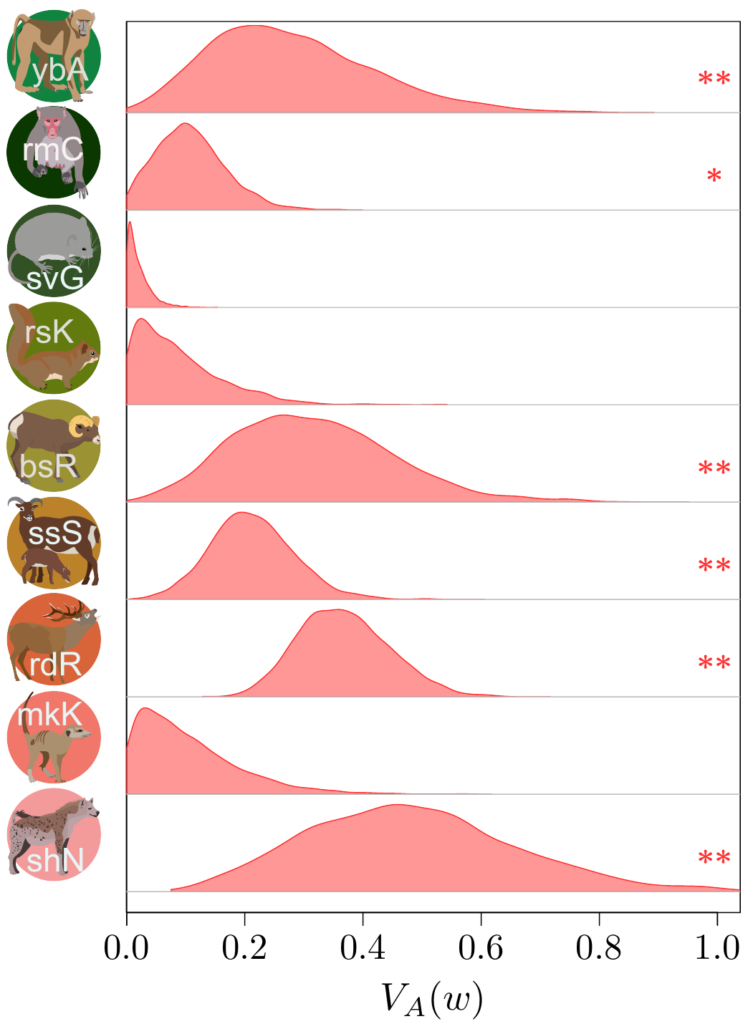
Bien sûr, calculer cette variance génétique additive n’a rien de facile… Ça demande l’information sur l’apparentement entre un grand (grand !) nombre d’individus dans la population, et bien sûr aussi, une bonne mesure de la valeur sélective. Très peu d’études sont suffisamment grosses, longues et détaillées pour ça…

Un autre problème, c’est que la valeur sélective est une quantité distribuée (au sens statistique) de manière très biscornue, avec un mélange de beaucoup de zéros et quelques valeurs extrêmement fortes (quelques individus avec un bien meilleur succès que les autres). Pendant longtemps, ce fait a été joyeusement ignoré, mais Timothée Bonnet, en collaboration avec Loeske Kruuk et Michael Morrissey, ont démontré que ne pas tenir compte de cette distribution exotique peut mener à des résultats assez peu corrects…. Mince. C’était une belle opportunité pour qu’on se mette tous ensemble avec les collègues. Sous la direction de Timothée et Loeske, nous (les collègues bossant sur en populations naturelles) nous avons rassemblés nos données toutes ensembles, pour voir que cette perspective moderne sur le vieux théorème de Fisher pouvait nous dire sur l’adaptation.

En plus de contribuer les données hihi, avec les copains de Nouvelle Zélande, j’ai aussi partagé à Timothée mon code pour venant de mon projet comparatif à moi, pour calculer des « méta-estimateurs » sur l’ensemble des jeux de données différents. J’ai aussi aidé à l’interprétation des résultats… dans la mesure de mes moyens bien sûr !

Estimation de la variance génétique additive de la valeur sélective dans 19 populations d’oiseaux et de mammifères
(depuis Bonnet et al., Science, 2022).

Les résultats (que vous pouvez découvrir dans notre article publié dans Science !) étaient finalement plutôt surprenants. Il semble qu’en raison de ce petit problème statistique (au moins dans une certaine mesure) que j’ai mentionnée plus haut à propos de la distribution statistique de la valeur sélective, on aurait auparavant sous-estimé de manière assez importante l’ampleur de l’évolution adaptative qui se produit dans les populations nautrelles… par un facteur de 2 à 4 ! C’est assez stupéfiant ! Ce qui est très frustrant avec ce type d’analyse, par contre, c’est qu’on ne peut pas vraiment dire ce qui est en train de s’adapter, ni même si de l’adaptation se produit à long terme (c’est important, vous l’aurez noté, c’est en gras, c’est clair, non ?). L’adaptation « instantanée » que nous déduisons de nos estimations des variances génétiques additives pourrait très bien concerner des traits cachés (comme les traits physiologiques), ou une multitude de changements minuscules dans un vaste ensemble de traits, ou même encore des changements qui fluctuent dans un sens puis dans l’autre, et qui donc ne se traduisent jamais par une évolution mesurable des traits phénotypiques dans le temps.

Étiquettes :