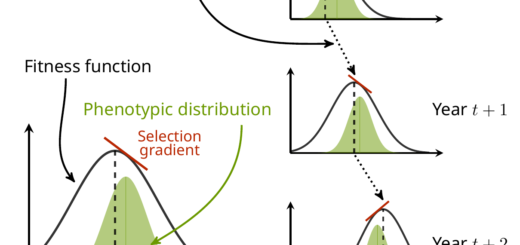
There is more evolution than we previously thought in wild populations
This fact is not very well-known to a wide audience, but the theory behind evolutionary biology is very much mathematised. For example, a theorem known as “The Price equation” describes very generally how biological features are expected to evolve in response to selection.
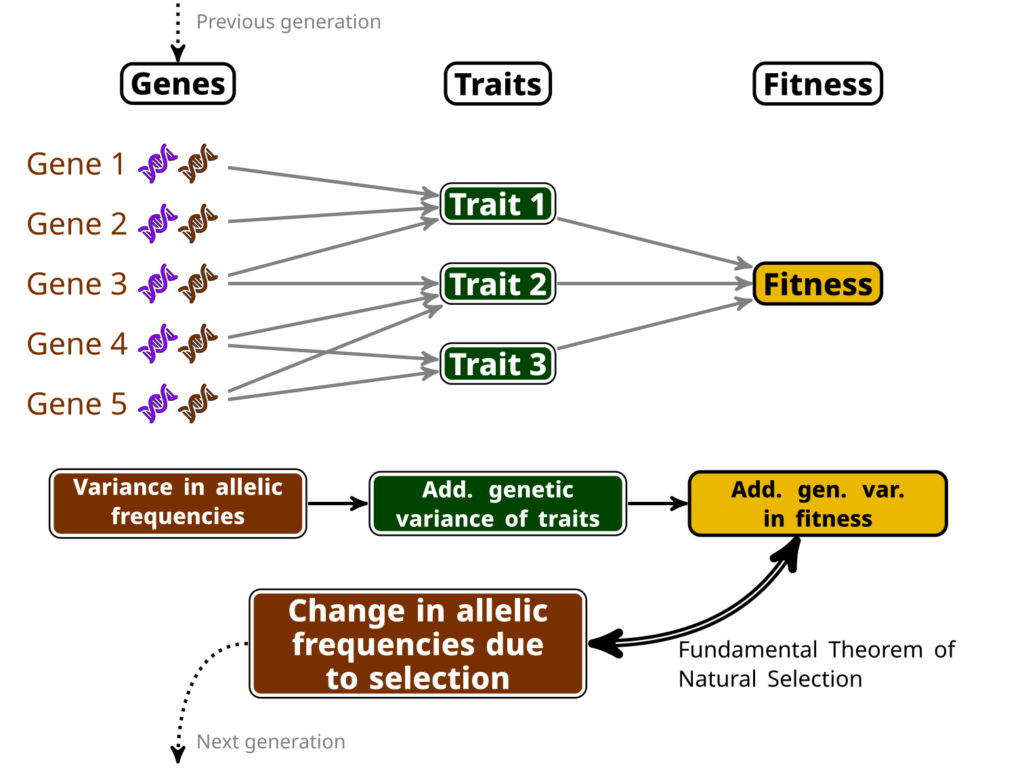
Ronald Fisher has been one of the earliest champion of a mathematicised theory of evolution (among other much more embarrassing things he championed…), and has even named (somewhat pompously) an equation the “Fundamental Theorem of Natural Selection”. This theorem has been the object of much debate and interpretation, but my favourite (a bit simple, but not too wrong) interpretation of it is that we can know the amount of change at the genetic level induced by selection by computing the amount of variance in (relative) fitness that can be transmitted to the next generation, which we name “additive genetic variance of relative fitness”.
In other words, if you can compute this additive genetic variance of relative fitness, you directly have an estimate of how much adaptation (in the sense of change in the allele frequencies at the genetic level due to selection) happens between a generation to the next. This is, because this variance is linked to the variance in allelic frequencies of “selected genes” (i.e. genes which variation impacts traits that are important for selection). See my little infography below as a clumsy attempt to make this clearer…
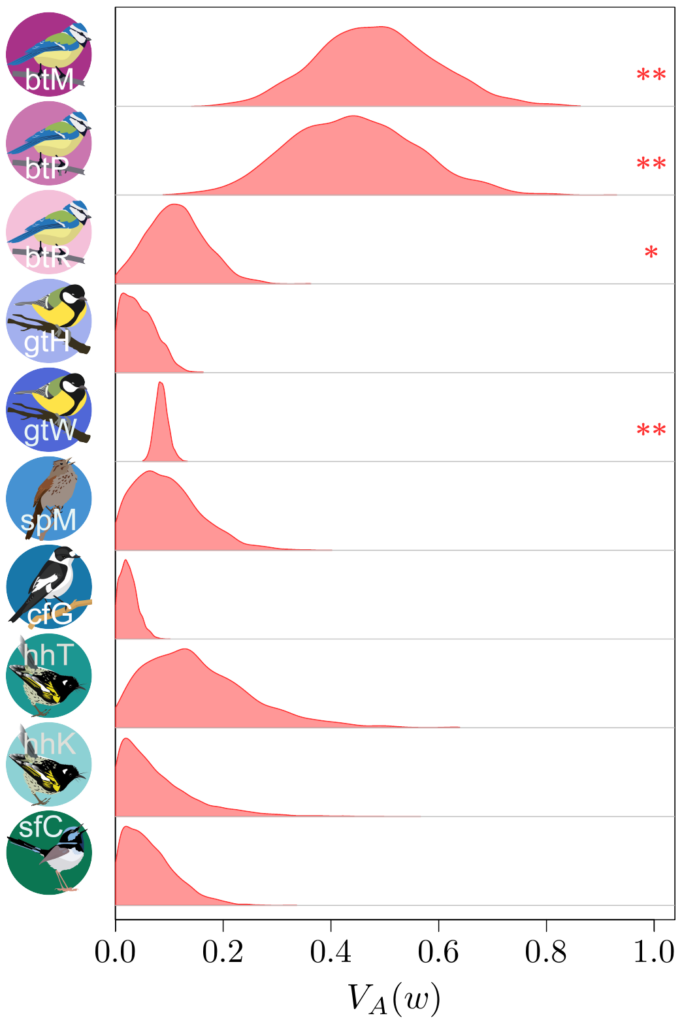
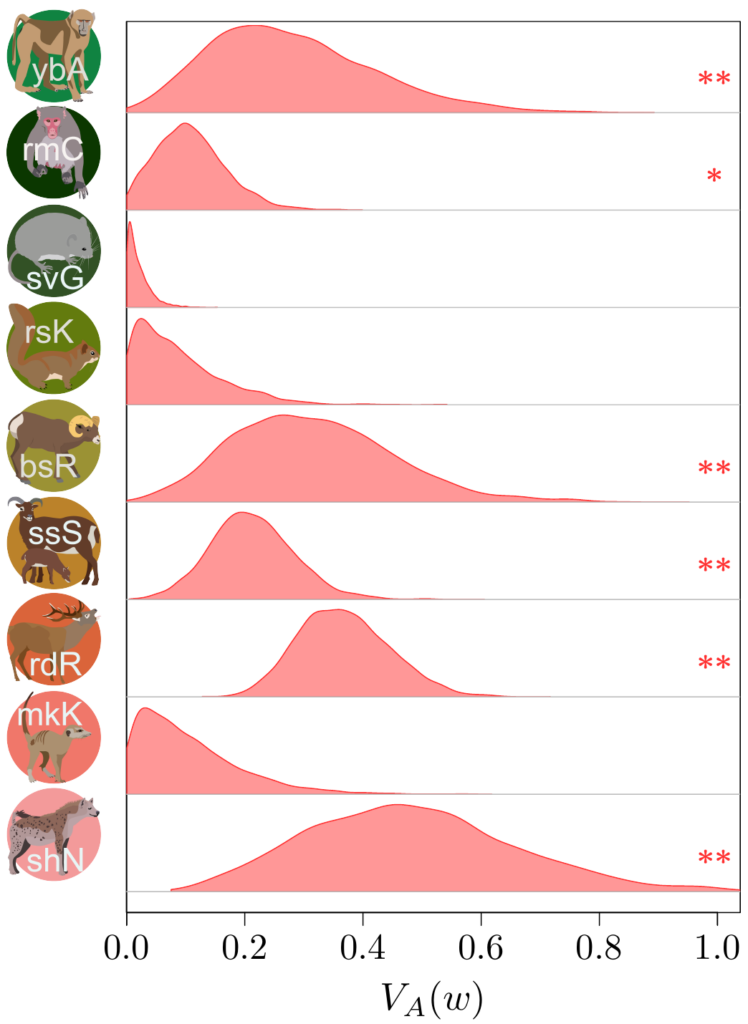
Now, computing additive genetic variances is no easy feat: you’ll need information about the relatedness between a lot (and I do mean, a lot!) of individuals within a population, and a proper measure of their fitness as well. Few surveys have enough information on the individuals, over a sufficiently long period of time, to do so…
Not only that, but fitness is very often an extremely weirdly distributed (in the statistical sense) trait. It has both a lot of zeros and some extremely large values (individuals that are much more successful than the others). For a long time, this fact had been merrily ignored, but Timothée Bonnet, in collaboration with Loeske Kruuk and Michael Morrissey, demonstrated that not accounting for such eccentric distribution would lead to quite incorrect results…. Oh, well. It was a good opportunity to join our efforts altogether with a lot of other people. Under Timothée’s and Loeske’s leadership, we (colleages working on wild populations) gathered our data together in order to find out what this modern perspective on the old Fisher’s theorem could tell us.

Besides contributing the hihi data, with my New Zealand friends, I also provided Timothée some code from my own such comparative project, to compute “meta-estimates” across all the different datasets, and helped in the interpretation of the results… to the best of my abilities, that is!
The results (which you could find more about in our paper in Science!) were actually quite surprising. It seems that (at least to quite a strong extent) because of this statistical shenanigan I mentioned earlier about the statistical distribution of fitness, we previously under-estimated quite strongly how much adaptive evolution happens in wild populations… by a factor 2 to 4! This is quite stunning! What is very frustrating however, from such analysis, is that we cannot really tell what is being adapted, or even whether adaptation is occurring over the long-term at all (this is important, as you’ve noted, it’s in bold, you got it, right?). The “ongoing adaptation” that we infer from our additive genetic variances estimates could very well be about hidden traits (like physiological traits), about a multitude of tiny changes in a vast set of traits, or even changes that are fluctuating back-and-forth, and thus never translating into any kind of measurable evolution in phenotypic traits over time.